Quantum Mechanics
Physics 137, Fall 2000
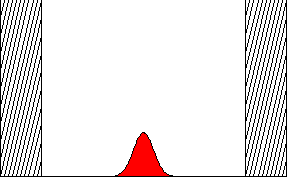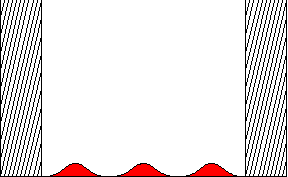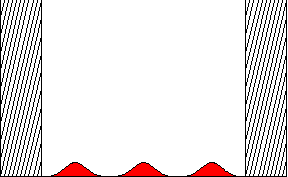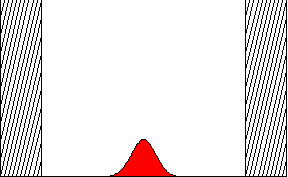
Temporal evolution of a wave packet in an infinite square well. This animated plot shows the probability of finding a particle as a function of position inside the well. At t=0, the wave packect has width a/10 (where a is the size of the well), and is localized at the center of the well. The wave packet has no net momentum p, thus, the center of the wave packet does not move. However, since we know the approximate position of the packet at t=0, by the uncertainty principle, there must be a spread in the momentum. Thus the packet spreads out, although it eventually reforms. (This is known in the lingo as "collapse and revival.")
When and where: MWF 9-10, 329 LeConte.
Instructor: Assistant Professor D. Budker. Office: 219 Birge, Labs: B217, 217, 221, 230 Birge, tel. 643-1829, e-mail: budker@socrates.Berkeley.edu, research group web page: http://socrates.berkeley.edu/~budker/
Office hour: Tu, 1-2PM, 219 Birge
Teaching Assistant: Uday Varadarajan. Office: 279 LeConte, tel. 642-5647 (office), 666-0728 (home), e-mail: udayv@socrates.berkeley.edu
Office hours: Tu, Th 11AM-12PM, and Fr 1-2PM.
Discussion Section: 101 Tuesday, 5-6 pm 329 LeConte
Course Outline: click here
Books:
Required text:
Griffiths, David J. Introduction to quantum mechanics. Englewood Cliffs, N.J. : Prentice Hall, 1995. QC174.12 .G75
Additional references:
History of QM
1. Segrè, Emilio. From x-rays to quarks : modern physicists and their discoveries. W. H. Freeman, 1980. QC7 .S4413
2. Ryutova-Kemoklidze, Margarita. The quantum generation: highlights and tragedies of the golden age of physics. New York : Springer, 1995. QC7 .R9613
Mathematics
1. Byron, Frederick W. and Fuller, Robert W. Mathematics of classical and quantum physics, QC20 .B9
Atomic physics
1. Bransden, B. H. and Joachain, C. J. Physics of Atoms and Molecules. Longman, 1988.
Advanced textbooks
1. Landau, L. D., and Lifshitz, E. M. Quantum mechanics : non-relativistic theory. Oxford ; New York : Pergamon Press, 1977. QC174.12 .L35131
2. Davydov, A. S. Quantum mechanics. 2d ed. Oxford ; New York : Pergamon Press, 1976. QC3 .I625 v.1 1976
3. Migdal, A. B. Qualitative methods in quantum theory. Addison-Wesley Publishing Co., The Advanced Book Program, 1989. QC174.12 .M53131
4. Edmonds, A. R. Angular momentum in quantum mechanics. Princeton University Press, 1974. QC174.1 .E3 1974
5. Bethe, H. A. and Salpeter, E. A . Quantum Mechanics of One- and Two-electron Atoms. Plenum 1977. QC 174.17.P7 B471 Reserve
Other books really worth reading
1. Feynman, R. P., Leighton, R. B., and Sands, M. The Feynman lectures on physics, v. 3, Addison-Wesley, Reading, Mass., UCB Physics QC22 .F47
Do not miss the lectures by Prof. William Phillips (1997 Nobel Prize winner for laser trapping and cooling)
Midterm #1: problems and solutions
Sign up for the class e-mail list: send us your e-mail address!
Midterm #2: review problems and solutions
Midterm #2: problems and solutions
Midterm # 2: Uday's review notes
Final: Uday's review notes
Final: Uday's review problems
Final: review_notes II and solutions to review problems
Seminars and Colloquia
Physics 290 F "Atomic" Seminar
LBNL Nuclear Science Division Colloquia
Physics Department Colloquia, Seminars, and Special Events
Lecture Notes, Electronic Tutorials
MathematicaTM notebook: Particle in an infinite square well Download MathReader from 
An HTML version of the above
MathematicaTM notebook: Two-level quantum mechanical system with periodic perturbation - elementary tutorial
Useful Links, Web Resources
Physics124: Introductory Nuclear Physics
Physics 250: Selected hot, cool, and ultracold topics in modern atomic physics
LBNL Table of Isotopes and related links
Glossary of Nuclear Terms
Web Elements Periodic Table
Nuclear Science Division, LBNL
Particle Data Group (PDG)
Coefficients
Radioactivity and radiation protection (from PDG)
Some web pages on phase and group velocities (found by Schuyler Kain):
Group Velocity and Phase Velocity
Dispersion
Some links that may help you with
Spherical Bessel functions
Neutrino oscillations: links galore
Los Alamos Science: look for special issue -- "Celebrating the Neutrino"
Homework
General advice and policy Contact the reader (person) Download Reader (program)
Reader (program)
Acknowledgment and Disclaimer: This material is based in part upon work supported by the National Science Foundation under Grant No. PHY-9733479. Any opinions, findings and conclusions or recomendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation (NSF).
